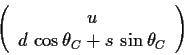 |
(6.1) |
Das Dublett der Quarks, das dem Dublett der Leptonen aus
Abb. 6.2 entspricht ist also:
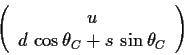 |
(6.1) |
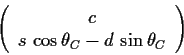 |
(6.2) |
6.5 Laufende Kopplung und asymptotische Freiheit
Das Laufen der Kopplung ist aus der
Callan-Symanzik-Gleichung bestimmt zu:
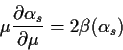 |
(6.3) |
In der Störungstheorie ergibt sich
![]() zu:
zu:
| (6.4) |
mit
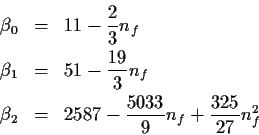
|
Nimmt man nur die niedrigste Näherung, ![]() , so erhält
man leicht:
, so erhält
man leicht:
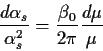 |
(6.5) |
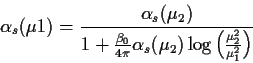 |
(6.6) |
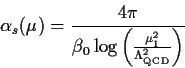 |
(6.7) |
Die Verwendung der laufenden Kopplung bei der Skala ![]() entspricht einer
Aufsummation aller Potenzen von
entspricht einer
Aufsummation aller Potenzen von
![]() . Leider
hängt diese ,,Renormierungsgruppenverbesserung'' in einigen Fällen auch von
der Wahl des gewählten Renormierungsschemas ab. Das für viele Fälle
bequemste Schema ist das sogenannte
. Leider
hängt diese ,,Renormierungsgruppenverbesserung'' in einigen Fällen auch von
der Wahl des gewählten Renormierungsschemas ab. Das für viele Fälle
bequemste Schema ist das sogenannte ![]() (sprich MS-bar) Schema.
MS steht für Minimal Subtraction.
(sprich MS-bar) Schema.
MS steht für Minimal Subtraction.
![]() Für die QED gilt in niedrigster
nichtverschwindender Näherung:
Für die QED gilt in niedrigster
nichtverschwindender Näherung:
![]() ,
also ist
,
also ist
![]() und die QED Kopplung wächst mit wachsender
Energie-Skala (abnehmenden Abstand); sie ist also nicht asymptotisch frei. Die
natürliche untere Schranke für die Skala ist hier die Elektronenmasse
und die QED Kopplung wächst mit wachsender
Energie-Skala (abnehmenden Abstand); sie ist also nicht asymptotisch frei. Die
natürliche untere Schranke für die Skala ist hier die Elektronenmasse ![]() .
Bei Beschränkung auf
.
Bei Beschränkung auf ![]() erhalten wir:
erhalten wir:
mit
![]() .
.
Der Ausdruck (6.8 hat eine Singularität bei
![]() . Dies ist der sogenannte Landau-Pol
bei einer Energie von
. Dies ist der sogenannte Landau-Pol
bei einer Energie von ![]() GeV !!, dagegen ist die Planck-Masse winzig.
GeV !!, dagegen ist die Planck-Masse winzig.
Die Strahlungskorrekturen der QED allein erhöhen die laufende
elektromagnetische Kopplung ![]() bei der Skala der
bei der Skala der ![]() -Masse um etwa 2%.
-Masse um etwa 2%.
6.7 Quantenchromodynamik auf dem Gitter
Sei ![]() ein Gitterpunkt und
ein Gitterpunkt und ![]() ein benachbarter
Punkt in
ein benachbarter
Punkt in ![]() -Richtung;
-Richtung; ![]() ist der Abstand zwischen den Gitterpunkten. Hat
also etwa
ist der Abstand zwischen den Gitterpunkten. Hat
also etwa ![]() die Koordinaten (0,0,0,0) und ist
die Koordinaten (0,0,0,0) und ist ![]() , dann hat
, dann hat ![]() die
Koordinaten
die
Koordinaten ![]() .
.
![]() ist ein Fermionfeld an einem Gitterpunkt
ist ein Fermionfeld an einem Gitterpunkt ![]() und
und ![]() bezeichne ein link von
bezeichne ein link von ![]() nach
nach ![]() .
.
![]() ist ein Element der Eichgruppe, für die Elektrodynamik,
ist ein Element der Eichgruppe, für die Elektrodynamik, ![]() , gilt
, gilt
Der wesentlichen Anteile
der Wechselwirkung auf dem Gitter ist gegeben einmal durch den reinen
Eichfeldanteil
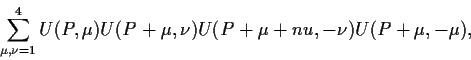 |
(6.10) |
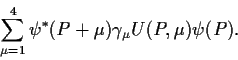 |
(6.11) |
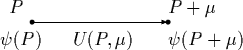 |
Die Gitter-QCD wird auf einer Euklidischen Raum-Zeit
definiert, diese erhält man aus der Minkowskischen durch die Ersetzung der
Zeit durch eine imaginäre Grösse (ja, die gute alte ![]() -Metrik):
-Metrik):
| (6.12) |