7.3 Die grosse Einheit
Eine Familie hat 15 Fermionen: 12 Quarks (2 Quarks und 2
Antiquarks in jeweils 3 Farben), Lepton, Antilepton und Neutrino. Um definiert
zu sein, betrachten wir die Familie von ![]() -Quarks,
-Quarks, ![]() und
und ![]() .
.
Im Modell von Georgi und Glashow (![]() ) bilden die 3
) bilden die 3 ![]() und 3
und 3 ![]() -Quarks,
die 3
-Quarks,
die 3 ![]() -Antiquarks und das Positron die Basis einer 10-dimensionalen
Darstellung. Die
-Antiquarks und das Positron die Basis einer 10-dimensionalen
Darstellung. Die ![]() -Antiquarks, Elektron und das Neutrino die Basis einer
5-dimensionalen Darstellung.
-Antiquarks, Elektron und das Neutrino die Basis einer
5-dimensionalen Darstellung.
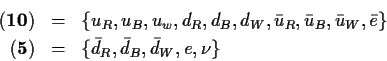
In einer ![]() sind diese mit einem
Antineutrino zu einer 16-dimensionalen Basis zusammengefasst.
sind diese mit einem
Antineutrino zu einer 16-dimensionalen Basis zusammengefasst.
Die Supersymmetrie
Die einfachste Supersymmetrische Algebra ist gegeben durch
die 4 Erzeugenden der Translationen in Raum und Zeit, d.i. der Energieoperator
![]() und die Impulsoperatoren
und die Impulsoperatoren
![]() sowie einen Fermionischen Operator
sowie einen Fermionischen Operator
![]() mit den (Anti)-Vertauschungsrelationen:
mit den (Anti)-Vertauschungsrelationen:
| (7.1) | |||
7.7 Ruhige Saiten
Die Gleichung für die Auslenkung ![]() einer
schwingenden Saite lautet:
einer
schwingenden Saite lautet:
Die Wellengeleichung 7.2 hat die allgemeine Lösung (d'Alembert):
| (7.3) |