5.1 Der Eichmeister
Wenn eine Wellenfunktion mit einem Phasenfaktor, d.h.
einer konstanten komplexen Zahl vom Betrag 1, multipliziert wird, so
beschreibt sie immer noch den gleichen physikalischen Zustand. Die
Phasenfaktoren,
![]() reell, sind Elemente der
reell, sind Elemente der ![]() , d.h.
wir könne das so ausdrücken: die Quantenmechanik ist invariant unter
, d.h.
wir könne das so ausdrücken: die Quantenmechanik ist invariant unter
![]() -Transformationen. Weyl fand es nun unplausibel, dass
-Transformationen. Weyl fand es nun unplausibel, dass ![]() tatsächlich eine Konstante sein muss, selbst wenn die Wellenfunktion sich
über noch so grosse Gebiete erstreckt. Er nannte dies einen Fernparallelismus,
der zu verwerfen sei.Er forderte daher, dass aus der Wellenfunktion auch
noch die gleiche Physik folge, wenn der Phasenfaktor von Raum und Zeit
abhängt, also die Wellenfunktion mit
tatsächlich eine Konstante sein muss, selbst wenn die Wellenfunktion sich
über noch so grosse Gebiete erstreckt. Er nannte dies einen Fernparallelismus,
der zu verwerfen sei.Er forderte daher, dass aus der Wellenfunktion auch
noch die gleiche Physik folge, wenn der Phasenfaktor von Raum und Zeit
abhängt, also die Wellenfunktion mit
![]() multipliziert wird. Die Verwerfung des Fernparallelismus bedeutet: Die
Wellenfunktion
multipliziert wird. Die Verwerfung des Fernparallelismus bedeutet: Die
Wellenfunktion ![]() und die ,,umgeeichte'' Wellenfunktion
und die ,,umgeeichte'' Wellenfunktion
![]() beschreiben die gleiche physikalische Situation.
Dies scheint unmöglich, denn die Wellenfunktion eines freien Fermions
beschreiben die gleiche physikalische Situation.
Dies scheint unmöglich, denn die Wellenfunktion eines freien Fermions ![]() genügt einer linearen Differentialgleichung, der Dirac-Gleichung
(1.12):
genügt einer linearen Differentialgleichung, der Dirac-Gleichung
(1.12):
Dass die ![]()
![]() -Matrizen sind, spielt hier keine
Rolle. Wenn Ihnen Matrizen unsympathisch (weil nicht vertraut) sind, können
sie für diese überlegung auch annehmen, die
-Matrizen sind, spielt hier keine
Rolle. Wenn Ihnen Matrizen unsympathisch (weil nicht vertraut) sind, können
sie für diese überlegung auch annehmen, die ![]() -Matrizen seien einfache
Zahlen.
-Matrizen seien einfache
Zahlen.
Wenn die Umeichung:
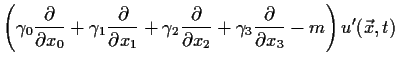 |
(5.3) | ||
![$\displaystyle \Bigg(\gamma _0 [\frac{\partial }{ \partial x_0}u(\vec x, t)+
i\,e\,u(\vec x, t) \frac{\partial }{\partial x_0}\lambda (\vec x,t)]$](img221.gif) |
|||
![$\displaystyle \gamma _1 [\frac{\partial }{ \partial x_1}u(\vec x, t)+
i\,e\,u(\vec x, t) \frac{\partial }{\partial x_1}\lambda (\vec x,t)]$](img223.gif) |
|||
![$\displaystyle \gamma _2 [\frac{\partial }{ \partial x_2}u(\vec x, t)+
i\,e\,u(\vec x, t) \frac{\partial }{\partial x_2}\lambda (\vec x,t)]$](img224.gif) |
|||
![$\displaystyle \gamma _3 [\frac{\partial }{ \partial x_3}u(\vec x, t)+
i\,e\,u(\...
...rtial x_3}\lambda (\vec x,t)] - m \,u(\vec x, t)\Bigg)
e^{i \lambda (\vec x,t)}$](img225.gif) |
|||
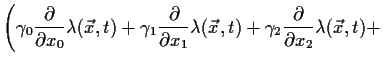 |
(5.4) | ||
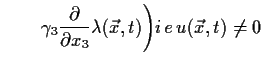 |
Dies geschieht, indem wir die Gleichung modifizieren, und zwar zu:
Wenn die Wellenfunktion gemäss 5.2 umgeeicht wird und gleichzeitig
noch das neu eingeführte 4-Vektor Feld ![]() auf folgende Weise
umgeeicht wird:
auf folgende Weise
umgeeicht wird:
Nun ist aber 5.6 gerade die altbekannte
Umeichung des 4-Potentials in der Elektrodynamik, bestehend aus dem
elektrischen Potential ![]() und dem magnetischen Vektorpotential
und dem magnetischen Vektorpotential ![]() ;
(5.5) ist die Dirac-Gleichung für ein geladenes Teilchen in einem
elektromagnetischen Feld. Dies ist die erfolgreiche Gleichung die auf Anhieb
das Problem der Feinstruktur im H-Atom löst und das richtige gyromagnetische
Verhältnis des Elektrons ergibt. Wir sehen also, wenn wir nur
Invarianz unter der Umeichung (5.2) fordern, dann folgt die Existenz des
elektromagnetischen Feldes und seine Wechselwirkung mit einem geladenen
Teilchen, beschrieben durch Gleichung (5.5).
Das elektrische und das magnetische Feld wird von der Umeichung der
Potentiale (5.6) nicht beeinflusst.
Ich gebe hier nur die 1-Komponente des elektrischen (
;
(5.5) ist die Dirac-Gleichung für ein geladenes Teilchen in einem
elektromagnetischen Feld. Dies ist die erfolgreiche Gleichung die auf Anhieb
das Problem der Feinstruktur im H-Atom löst und das richtige gyromagnetische
Verhältnis des Elektrons ergibt. Wir sehen also, wenn wir nur
Invarianz unter der Umeichung (5.2) fordern, dann folgt die Existenz des
elektromagnetischen Feldes und seine Wechselwirkung mit einem geladenen
Teilchen, beschrieben durch Gleichung (5.5).
Das elektrische und das magnetische Feld wird von der Umeichung der
Potentiale (5.6) nicht beeinflusst.
Ich gebe hier nur die 1-Komponente des elektrischen (![]() ) und magnetischen
(
) und magnetischen
(![]() ) Feldes an:
) Feldes an:
| (5.7) |
Fassen wir zusammen: Es gibt unbestritten in der Quantenmechanik eine Symmetrie: Multipliziert man die Wellenfunktionen mit einem Phasenfaktor, also einer komplexen Zahl vom Betrag 1, so ändert dies nichts an den Ergebnissen. Fordert man, dass die Symmetrie auch gilt, wenn der Phasenfaktor an jedem Punk des Raum-Zeit-Kontinuums andere Werte annehmen kann, also eine beliebige Funktion von Raum und Zeit-Koordinaten ist, so sagt man heute allgemein, man habe diese Symmetrie geeicht. Die verschärfte Forderung nach Eichsymmetrie führt zu weitreichenden dynamischen Konsequenzen: Es muss ein neues Feld, hier neben dem Materiefeld für die geladenen Teilchen auch noch das elektromagnetische Feld eingeführt werden, und die Wechselwirkung des neuen Feldes mit den bisherigen ist auch schon festgelegt.
Die Wechselwirkung geladener Fermionen mit dem elektrischen Feld (1.18) folgt direkt aus (5.5).
5.2 Die Eichungen werden mehrdimensional
Die Transformationen der ![]() -Gruppe werden erzeugt
durch die Pauli-Matrizen
-Gruppe werden erzeugt
durch die Pauli-Matrizen ![]() (1.40),
d.h. ein Iso-Spinor
(1.40),
d.h. ein Iso-Spinor ![]() geht über in
geht über in
| (5.8) |
| (5.9) |
bei einer geeichten ![]() muss man wegen der 3 Erzeugenden auch 3
Eich-4-Potentiale:
muss man wegen der 3 Erzeugenden auch 3
Eich-4-Potentiale:
![]() einführen.
einführen.
Die Analoga der elektrischen und magnetischen Felder sind bei einer solchen
,,nichtabelschen Eichtheorie'' komplizierter, etwa für die 1-Komponente des
1. (von 3) ,,elektrischen'' Feldern:
| (5.10) |
Es ist der zusätzliche nichtlineare Term
![]() . der für die Kopplung der Eichbosonen
aneinander (Fig. 5.3a und b) verantwortlich ist.
. der für die Kopplung der Eichbosonen
aneinander (Fig. 5.3a und b) verantwortlich ist.
5.3 Spontane Symmetriebrechung
Wie im Haupttext erwähnt, fassen wir die beiden reellen
Felder ![]() und
und ![]() zu einem komplexen Feld zusammen:
zu einem komplexen Feld zusammen:
Das komplexe Feld ![]() zerlegen wir in den Betrag
zerlegen wir in den Betrag
![]() und die Phase
und die Phase
![]() :
:
| (5.12) |
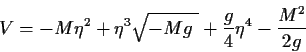 |
(5.13) |
Es taucht nur noch im kinetischen Beitrag zur
Feldenergie auf, und der liefert auch eine charakteristische Wechselwirkung des
![]() -Feldes mit dem
-Feldes mit dem ![]() -Feld. Das
-Feld. Das ![]() Feld hat
einen Masseterm
Feld hat
einen Masseterm ![]() , der positiv ist, da
, der positiv ist, da ![]() negativ ist.
negativ ist.
Wenn wir nun Störungstheorie in den Feldern ![]() und
und ![]() treiben, finden
wir den folgenden Teilcheninhalt:
treiben, finden
wir den folgenden Teilcheninhalt:
Ein Goldstone-Boson mit Masse 0, das Feldquant des ![]() -Feldes sowie ein
,,Higgs-Boson'' mit Masse
-Feldes sowie ein
,,Higgs-Boson'' mit Masse ![]() , das Feldquant des
, das Feldquant des ![]() -Feldes.
-Feldes.
5.4 Das Festmahl von Higgs und Kibble
Wird an das skalare Feld ![]() noch ein Eichfeld
angekoppelt (z.B. ein elektromagnetisches), so gibt es als Beitrag zur
statischen Feldenergie ausser den schon erwähnten Beiträgen noch den
zusätzlichen Wechselwirkungsterm des Feldes
noch ein Eichfeld
angekoppelt (z.B. ein elektromagnetisches), so gibt es als Beitrag zur
statischen Feldenergie ausser den schon erwähnten Beiträgen noch den
zusätzlichen Wechselwirkungsterm des Feldes ![]() mit dem Eichpotential
mit dem Eichpotential
![]() . Dieser Term ist :
. Dieser Term ist :
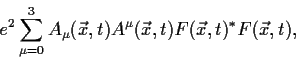 |
(5.14) |
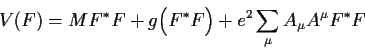 |
(5.15) |
Ersetzen wir nun wieder nach (5.11) ![]() durch
durch ![]() und
und ![]() ,
so erhalten wir:
,
so erhalten wir:
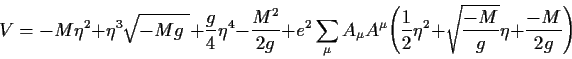 |
(5.16) |
Wir sehen, dass wir nun auch einen quadratischen Term im
Eichpotential haben,
nämlich
![]() . Die ist ein
Massenterm, das Eichfeld hat also eine Masse
. Die ist ein
Massenterm, das Eichfeld hat also eine Masse
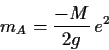
Das Goldstone Boson mit seinem Feld ![]() tritt zwar immer noch formal
auf, aber wir können es in diesem Falle der spontanen Symmetriebrechung
einer Eichsymmetrie wegeichen: Ersetzen wir nämlich (vgl.
5.2,5.6):
tritt zwar immer noch formal
auf, aber wir können es in diesem Falle der spontanen Symmetriebrechung
einer Eichsymmetrie wegeichen: Ersetzen wir nämlich (vgl.
5.2,5.6):
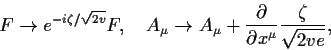 |
(5.17) |
5.6 Bessere Zähler, bessere Beschleuniger und bessere Strahlen
Die Gesamtenergie ![]() im Schwerpunktsystem ist gegeben
durch
im Schwerpunktsystem ist gegeben
durch
![]() . Im Laborsystem (ruhendes target) ist
. Im Laborsystem (ruhendes target) ist
![]() also
also
| (5.18) |
Werden dagegen die beiden Teilchen mit gleichem, aber entgegengesetzt gerichteten
Impuls beschleunigt, also
![]() , dann ist
, dann ist
| (5.19) |
5.7 Die Elektronenmikroskope
der Elementarteilchenphysik
Beim elastischen Zusammenstoss zweier Teilchen ist die
maximale Impulsübertragung:
| (5.20) |
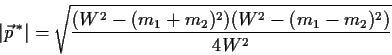 |
(5.21) |
| (5.22) |
5.8 Tief inelastische Streuung
Entscheidend für die Analyse der tiefinelastischen Streuung ist das optische Theorem: Der untere Teil des Graphen von Abb. 5.13 kann als die Streuung eines virtuellen Photons mit einem Proton betrachtet werden, der obere Teil ist aus der QED bekannt. Daher misst man sozusagen in der tief inelastischen Streuung den totalen Wirkungsquerschnitt für die Streuung eines virtuellen Photons an einem Proton. Dieser totale Querschnitt ist wiederum proportional dem Imaginärteil der Vorwärtsstreuamplitude, die man theoretisch analysiert.
Im Detail ist die Behandlung der tiefinelastischen Streuung sehr kompliziert, da es aufgrund des Spins und der verschiedenen Ströme (schwacher und elektromagnetischer) insgesamt 3 Strukturfunktionen gibt. Um sie zu bestimmen braucht man sehr detaillierte Messungen mit Elektronen oder Positronen und Neutrinos.