Ich benutze im Anhang meist die natürlichen Einheiten, also ![]() .
.
Wenn nicht ausdrücklich anders vermerkt ist mit der Energie immer die Energie einschliesslich der Ruhenergie gemeint.
1.2 Die Heile Welt
Zur Bestimmung von ![]() wird die Coulomb-Kraft des
Elektrischen Feldes
wird die Coulomb-Kraft des
Elektrischen Feldes ![]() und die Lorentz-Kraft des Magnetfeldes
und die Lorentz-Kraft des Magnetfeldes ![]() benutzt:
benutzt:
Coulomb-Kraft: ![]() in Richtung des E-Feldes
in Richtung des E-Feldes
Lorentz-Kraft:
![]() , senkrecht auf Richtungen von
, senkrecht auf Richtungen von ![]() und
und
![]() .
.
![]() ist die Geschwindigkeit des geladenen Teilchens,
ist die Geschwindigkeit des geladenen Teilchens, ![]() wie immer die
Lichtgeschwindigkeit im Vakuum.
wie immer die
Lichtgeschwindigkeit im Vakuum.
![]() Die Rutherfordsche Streuformel für Teilchen der
Masse
Die Rutherfordsche Streuformel für Teilchen der
Masse ![]() , der Ladung
, der Ladung ![]() und der Geschwindigkeit
und der Geschwindigkeit ![]() an einem sehr
schweren Kern lautet der Ladung
an einem sehr
schweren Kern lautet der Ladung ![]() :
:
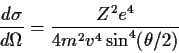 |
(1.1) |
1.3 Kontrolle ist besser
Der Energieverlust eines geladenen Teilchens der Ladung ![]() und Geschwindigkeit
und Geschwindigkeit ![]() durch Ionisation pro Längeneinheit ist nach
halbklassischen Überlegungen gegeben durch:
durch Ionisation pro Längeneinheit ist nach
halbklassischen Überlegungen gegeben durch:
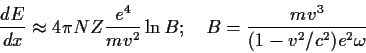 |
(1.2) |
Hierbei ist ![]() die Zahl der Elektronen pro Volumeneinheit des
ionisierten Materials,
die Zahl der Elektronen pro Volumeneinheit des
ionisierten Materials, ![]() eine für das Material typische Frequenz,
eine für das Material typische Frequenz, ![]() ist ungefähr die Ionisierungsenergie.
ist ungefähr die Ionisierungsenergie.
Für kleine Geschwindigkeiten (![]() ) gilt also
) gilt also
| (1.3) |
Für grosse
Geschwindigkeiten (![]() ) gilt:
) gilt:
| (1.4) |
1.4.1 Spezielle Relativitätstheorie und Quantenphysik
Was die gewöhnlichen 3-Vektoren für den Raum sind, sind
die 4-Vektoren für das
Raum-Zeit-Kontinuum:
| (1.5) |
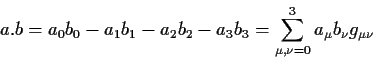 |
(1.6) |
(Etwas Matrix-Algebra wird ab (1.28) ff erläutert)
Lorentz-Transformationen lassen das 4-dimensionale Skalarprodukt ungeändert, wie Drehungen im Raum das 3-dimensionale.
Energie ![]() und Impuls
und Impuls
![]() bilden zusammen einen 4-Vektor:
bilden zusammen einen 4-Vektor:
| (1.8) |
Ebenso Zeit und Raumkoordinaten:
| (1.9) |
Das Skalarprodukt von ![]() mit sich selbst ist die Masse mal
mit sich selbst ist die Masse mal ![]() :
:
| (1.10) |
Der Zusammenhang zwischen Energie ![]() , 3-Impuls
, 3-Impuls ![]() und Geschwindigkeit
und Geschwindigkeit
![]() eines Teilchens mit Masse
eines Teilchens mit Masse ![]() ist demnach:
ist demnach:
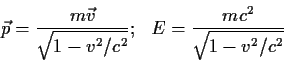 |
(1.11) |
![]() Die freie Dirac-Gleichung (d.h. ohne
elektromagnetische Felder) lautet:
Die freie Dirac-Gleichung (d.h. ohne
elektromagnetische Felder) lautet:
Der Spinor ![]() hat 4 Komponenten
hat 4 Komponenten
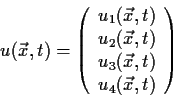 |
(1.14) |
Die Dirac-Gleichung für ein Teilchen im elektromagnetischen Feld wird in 5.1 (5.5 hergeleitet
1.4.2 Feldtheorie und Quantenphysik
Für das folgende ist es bequem einzuführen:
den Kommutator
| (1.15) |
| (1.16) |
Für die Erzeuger und Vernichter von Teilchen mit ganzzahligem Spin gilt:
| (1.17) |
Für Fermionen sind die Kommutatoren ![]() durch Antikommutatoren
durch Antikommutatoren ![]() zu
ersetzen.
zu
ersetzen.
![]() Die vollständige Form der Wechselwirkung ist, s.
(5.5):
Die vollständige Form der Wechselwirkung ist, s.
(5.5):
wobei ![]() das elektrische und
das elektrische und ![]() das magnetische (Vektor-) Potential
ist,
das magnetische (Vektor-) Potential
ist, ![]() ist die Ladung des Teilchens.
ist die Ladung des Teilchens.
![]() Eine innere Linie eines Quantenfeldes (der sog.
Propagator) der Masse
Eine innere Linie eines Quantenfeldes (der sog.
Propagator) der Masse ![]() gibt Anlass zu einem Faktor:
gibt Anlass zu einem Faktor:
![]() ,
wobei
,
wobei ![]() der von der inneren Linie getragene 4-Impuls ist.
der von der inneren Linie getragene 4-Impuls ist.
Der Austausch eines Teilchens mit der Masse ![]() gibt daher
einen Faktor:
gibt daher
einen Faktor:
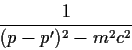 |
(1.19) |
Durch Fouriertransformation folgt daraus bei kleinen Geschwindigkeiten
(d.h. nichtrelativistisch) für das Wechselwirkungspotential:
| (1.20) |
Für das Photon (Masse 0) folgt daraus das bekannte Coulomb-Potential, für
den Austausch von Mesonen das Yukawa-Potential mit der Reichweite
![]()
Der Faktor
![]() , der beim Austausch eines Photons auftritt,
ist auch Anlass für den Term
, der beim Austausch eines Photons auftritt,
ist auch Anlass für den Term
![]() bei der
Rutherford-Streuung.
bei der
Rutherford-Streuung.
![]() Der Quantenkorrektur von Abb. 1.13a (Selbstenergie)
entspricht das divergente Integral:
Der Quantenkorrektur von Abb. 1.13a (Selbstenergie)
entspricht das divergente Integral:
| (1.21) |
![]() Thomson hatte schon 1904 den Wirkungsquerschnitt für die
Streuung von Licht an Elektronen mit Hilfe der klassischen Elektrodynamik
berechnet. Er hatte natürlich den Fluss nicht als Fluss von Teilchen,
sondern als Energiefluss betrachtet. Man kann die beiden aber leicht
umrechnen, da ein Photon die Energie
Thomson hatte schon 1904 den Wirkungsquerschnitt für die
Streuung von Licht an Elektronen mit Hilfe der klassischen Elektrodynamik
berechnet. Er hatte natürlich den Fluss nicht als Fluss von Teilchen,
sondern als Energiefluss betrachtet. Man kann die beiden aber leicht
umrechnen, da ein Photon die Energie
![]() hat.
hat.
Der Thomsonsche Wirkungsquerschnitt ist:
Die Graphen von Abb. 1.9 führen in
der Grenze verschwindenden Photonenimpulses genau zum Wirkungsquerschnitt
1.22, wenn man für die Ladung ![]() die klassische Ladung einsetzt.
In diesem Falle tragen also die Quantenkorrekturen nicht bei, sondern erst bei
höheren Photon-Impulsen.
die klassische Ladung einsetzt.
In diesem Falle tragen also die Quantenkorrekturen nicht bei, sondern erst bei
höheren Photon-Impulsen.
1.4.3 Quantenphysik und Fehler
Obwohl die Quantenmechanik eine deterministische Theorie ist, macht sie nur Wahrscheinlichkeitsaussagen, und deshalb werden die Ergebnisse von Messungen i. a. streuen.
Ganz allgemein gilt: Ist ![]() die Wahrscheinlichkeit für das Eintreten eines
Ereignisses
die Wahrscheinlichkeit für das Eintreten eines
Ereignisses ![]() und liegen insgesamt
und liegen insgesamt ![]() Möglichkeiten des Eintretens vor,
dann ist die Wahrscheinlichkeitsverteilung der Messwerte
Möglichkeiten des Eintretens vor,
dann ist die Wahrscheinlichkeitsverteilung der Messwerte ![]() :
:
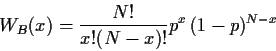 |
(1.23) |
Für unser Beispiel: Ist ![]() die Gesamtzahl der instabilen Teilchen und
die Gesamtzahl der instabilen Teilchen und
![]() die Wahrscheinlichkeit dafür , dass ein Teilchen innerhalb einer Sekunde
zerfällt , dann ist
die Wahrscheinlichkeit dafür , dass ein Teilchen innerhalb einer Sekunde
zerfällt , dann ist ![]() die Wahrscheinlichkeitsverteilung dafür, dass ich
in einer Sekunde
die Wahrscheinlichkeitsverteilung dafür, dass ich
in einer Sekunde ![]() Zerfälle registriere (angenommen, jeder Zerfall bringt
meine Messapparatur zum Ansprechen).
Zerfälle registriere (angenommen, jeder Zerfall bringt
meine Messapparatur zum Ansprechen).
Für den wichtigen Spezialfall, dass ![]() sehr
klein und
sehr
klein und ![]() sehr gross ist, geht diese ,,Binomialverteilung'' über in die
,,Poisson-Verteilung'':
sehr gross ist, geht diese ,,Binomialverteilung'' über in die
,,Poisson-Verteilung'':
| (1.24) |
Nahe dem Mittelwert ![]() kann man diese Poisson-Verteilung auch durch
eine Normal- oder Gauss-Verteilung approximieren:
kann man diese Poisson-Verteilung auch durch
eine Normal- oder Gauss-Verteilung approximieren:
| (1.25) |
![]() wird als Standardabweichung bezeichnet. Mit einer Wahrscheinlichkeit von
etwa 2/3 liegt das aktuelle Messergebnis innerhalb des Bereiches
wird als Standardabweichung bezeichnet. Mit einer Wahrscheinlichkeit von
etwa 2/3 liegt das aktuelle Messergebnis innerhalb des Bereiches
![]() oder umgekehrt, mit der Wahrscheinlichkeit von
1/3 liegt die Wahrscheinlichkeit
oder umgekehrt, mit der Wahrscheinlichkeit von
1/3 liegt die Wahrscheinlichkeit ![]() ausserhalb des Bereiches
(
ausserhalb des Bereiches
(
![]() ), wobei
), wobei ![]() der aktuelle gemessene
Zahl der eingetretenen Ereignisse (z.B. Zerfälle oder Streuereignisse) ist.
der aktuelle gemessene
Zahl der eingetretenen Ereignisse (z.B. Zerfälle oder Streuereignisse) ist.
Wenn die mit Hilfe der Quantenmechanik exakt berechnete
Wahrscheinlichkeit für ein Ereignis ![]() ist, so werden die Ergebnisse von
Messreihen dennoch nach den oben angegebenen Verteilungen streuen. Um aus
Messergebnissen auf die Wahrscheinlichkeit
ist, so werden die Ergebnisse von
Messreihen dennoch nach den oben angegebenen Verteilungen streuen. Um aus
Messergebnissen auf die Wahrscheinlichkeit ![]() zu schliessen, muss ich die
Schwankungen berücksichtigen. Da die Standardabweichung
zu schliessen, muss ich die
Schwankungen berücksichtigen. Da die Standardabweichung
![]() ist, erhalte ich, mit
ist, erhalte ich, mit ![]() :
:
| (1.26) |
Der absolute Standardfehler ist also
![]() , der relative
Fehler, auf den es i. a. ankommt ist:
, der relative
Fehler, auf den es i. a. ankommt ist:
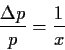 |
(1.27) |
1.5.1 Symmetrien und Transformationen
Eine Gruppe ist eine Menge ![]() von
Elementen,
von
Elementen,![]() , für die es eine Verknüpfung
, für die es eine Verknüpfung ![]() - i. a.
Multiplikation genannt - gibt, mit den folgenden Eigenschaften:
- i. a.
Multiplikation genannt - gibt, mit den folgenden Eigenschaften:
![]() Matrizen:
Allgemeine
Matrizen:
Allgemeine ![]() -dimensionale Matrix:
-dimensionale Matrix:
Produkt zweier Matrizen:
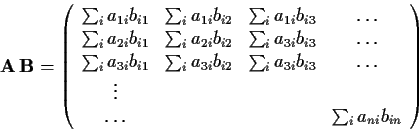 |
(1.29) |
Die Summe ![]() über
über ![]() geht von 1 bis
geht von 1 bis ![]() .
.
Die Anwendung einer ![]() -dimensionalen Matrix
-dimensionalen Matrix ![]() auf einen
auf einen ![]() -dimensionalen
Vektor
-dimensionalen
Vektor ![]() ergibt wieder einen Vektor:
ergibt wieder einen Vektor:
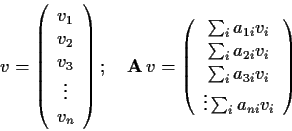 |
(1.30) |
Man definiert die adjungierte Matrix als das komplex Konjugierte und Transponierte:
Eine Matrix mit reellen oder komplexen Argumenten ![]() heisst unitär, wenn
heisst unitär, wenn
| (1.33) |
Beispiel: Drehung in einer Ebene um den Winkel ![]() .
.
Drehmatrix:
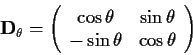 |
(1.34) |
Gedrehter Vektor von
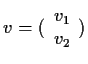 :
:
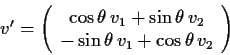 |
(1.35) |
Zwei Drehungen um die Winkel ![]() und
und ![]() hintereinander durchgeführt
ergeben
hintereinander durchgeführt
ergeben
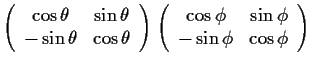 |
(1.36) | ||
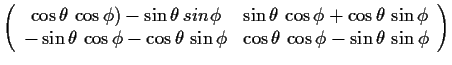 |
|||
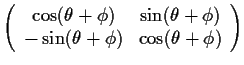 |
Für die Drehmatrizen gilt:
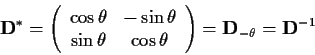 |
(1.37) |
Dies ist charakteristisch für die Drehung, da diese Eigenschaft garantiert, dass Längen von und Winkel zwischen Vektoren sich nicht ändern.
1.5.2 Das Wunder des Spins
![]() Genau genommen sind die Drehimpulsoperatoren die
Erzeugenden der Drehungen multipliziert mit
Genau genommen sind die Drehimpulsoperatoren die
Erzeugenden der Drehungen multipliziert mit ![]() .
.
Eine Drehung um die ![]() -Achse mit dem Winkel
-Achse mit dem Winkel ![]() lässt sich mit
Hilfe der erzeugenden
lässt sich mit
Hilfe der erzeugenden
![]() darstellen als:
darstellen als:
| (1.38) |
Die Exponentialfunktion von einem Operator lässt sich z.B. über
die Potenzreihe definieren:
| (1.39) |
Die Erzeugenden der ![]() ,
,
![]() sind
gegeben durch die Pauli-Matrizen:
sind
gegeben durch die Pauli-Matrizen:
Man kann direkt die Vertauschungsrelationen nachrechnen:
| (1.41) |
Die Drehung eines Spinors um die ![]() -Achse ist gegeben durch
(Potenzreihenentwicklung):
-Achse ist gegeben durch
(Potenzreihenentwicklung):
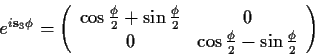 |
(1.42) |
Für
![]() ist
ist
![]() und
und
![]() ,
bei einer Drehung um
,
bei einer Drehung um
![]() ist also
ist also
![]() das Negative der Einheitsmatrix! Das heisst, dass bei einer vollen
Drehung um 360
das Negative der Einheitsmatrix! Das heisst, dass bei einer vollen
Drehung um 360![]() ein Spinor sein Vorzeichen ändert. Dies hat
experimentell bestätigte Konsequenzen.
ein Spinor sein Vorzeichen ändert. Dies hat
experimentell bestätigte Konsequenzen.
1.6 Die Entdeckung des Positrons und des ,,Mesotrons''
Ein geladenes Teilchen der Masse ![]() und Ladung
und Ladung ![]() bewege
sich mit dem Impuls
bewege
sich mit dem Impuls ![]() einem homogenen Magnetfeld.
Es gilt die Bewegungsgleichung:
einem homogenen Magnetfeld.
Es gilt die Bewegungsgleichung:
| (1.43) |
Für Geschwindigkeiten senkrecht zum Magnetfeld ergibt sich als Lösung eine
Kreisbahn mit Radius
Aus dem Krümmungsradius ![]() lässt sich also der Impuls bestimmen.
lässt sich also der Impuls bestimmen.
1.7 Frühe Beschleuniger
Für ![]() klein gegenüber der Lichtgeschwindigkeit
folgt aus 1.44
klein gegenüber der Lichtgeschwindigkeit
folgt aus 1.44
| (1.45) |
| (1.46) |
Für alle Geschwindigkeiten, auch ![]() nahe bei
nahe bei ![]() , gilt die
Beziehung:
, gilt die
Beziehung:
| (1.47) |
| (1.48) |