3.2 Streuamplituden
Der Wirkungsquerschnitt berechnet sich aus der
Streuamplitude ![]() als
als
| (3.1) |
Im System, in dem das Targetteilchen ruht gilt:
![]() , wobei
, wobei ![]() und
und ![]() Energie und Masse des
gestreuten Teilchens sind,
Energie und Masse des
gestreuten Teilchens sind, ![]() ist die Masse des Targetteilchens.
ist die Masse des Targetteilchens.
Der
Phasenraumfaktor ![]() ist das Mass aller Komponenten
der 4-Impulse, mit der Einschränkung, dass das Quadrat des Impulses gleich der
Masse des Teilchens ist und dass der Gesamtimpuls
ist das Mass aller Komponenten
der 4-Impulse, mit der Einschränkung, dass das Quadrat des Impulses gleich der
Masse des Teilchens ist und dass der Gesamtimpuls ![]() beim
Streuprozess erhalten ist; für
beim
Streuprozess erhalten ist; für ![]() Teilchen gilt also:
Teilchen gilt also:
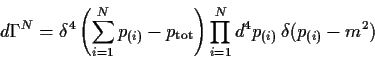 |
(3.2) |
![]() Sehr schematisch können wir uns die
Konsequenzen der Unitarität so klarmachen:
Sehr schematisch können wir uns die
Konsequenzen der Unitarität so klarmachen:
Die Unitarität der S-Matrix besagt, dass das Produkt der S-Matrix mit ihrem
hermitisch Adjungierten gleich der Einheitsmatrix ist:
Aus der Unitarität (3.3) folgt:
| (3.4) |
| (3.5) |
Aus letzter Gleichung folgt das optische Theorem, dass nämlich der totale Wirkungsquerschnitt gleich dem Imaginärteil der Streuamplitude in Vorwärtsrichtung ist.
Bei aktuellen Rechnungen spielt die Phasenraumdichte der streuenden Teilchen natürlich noch eine wichtige Rolle.
![]() Sei
Sei ![]() stets die Gesamtenergie und
stets die Gesamtenergie und ![]() der
Streuwinkel im Schwerpunktsystem des Prozesses, d.h. in dem System, in dem beide
zusammenstossende Teilchen gleichgrossen aber entgegengesetzt gerichteten
Impuls haben.
der
Streuwinkel im Schwerpunktsystem des Prozesses, d.h. in dem System, in dem beide
zusammenstossende Teilchen gleichgrossen aber entgegengesetzt gerichteten
Impuls haben.
Dann gilt für den Fall der pi-Meson-Nukleon-Streuung für
den Impuls und die Energie der einzelnen Teilchen im
![]() Schwerpunktsystem (Abb. 3.2.a):
Schwerpunktsystem (Abb. 3.2.a):
Für den Fall der Proton-Antiproton-Vernichtung in 2 ![]() -Mesonen, Abb. 3.2 b
gilt :
-Mesonen, Abb. 3.2 b
gilt :
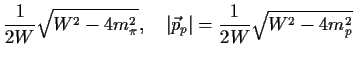 |
(3.10) | ||
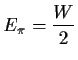 |
(3.11) |
Die Mandelstam Variablen für diesen Vernichtungsprozess sind:
Der Graph von Abb. 3.2.c hat für die pi-Meson-Nukleon-Streuung den
Polterm, vg. (3.8):
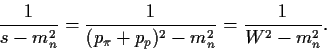 |
(3.14) |
Für die Vernichtung von Proton und Antiproton lautet der Polterm, vgl.
(3.12):
![\begin{displaymath}
\frac{1}{(p_p-p_{\pi^+})^2-m_n^2} =\frac{1}{m_p^2+m_\pi^2-
\...
...(W^2-\sqrt{[W^2-4 m_p^2][W^2-4m_\pi^2]}\cos\theta\bigg)-m_n^2}
\end{displaymath}](img203.gif) |
(3.15) |
3.4 Strenge Theoreme und komplexe Drehimpulse
Aus der axiomatischen Feldtheorie folgt für den totalen Wirkungsquerschnitt zweier Hadronen die Froissart-Martin Schranke:
| (3.16) |
![]() Bei der Fortsetzung der Drehimpulse ins Komplexe
ist der entscheidende Punkt, dass man die Summe über alle Partialwellen mit
Hilfe des Residuensatzes in ein Integral verwandelt und dann nach Deformation
des Integrationsweges die unendliche Summe durch einige Polterme ausdrückt.
Bei der Fortsetzung der Drehimpulse ins Komplexe
ist der entscheidende Punkt, dass man die Summe über alle Partialwellen mit
Hilfe des Residuensatzes in ein Integral verwandelt und dann nach Deformation
des Integrationsweges die unendliche Summe durch einige Polterme ausdrückt.
![]() Die Veneziano Amplitude für die elastische
Streuung von 2 gleichen Teilchen der Masse
Die Veneziano Amplitude für die elastische
Streuung von 2 gleichen Teilchen der Masse ![]() ist:
ist:
| (3.17) |
wobei die Eulersche Beta-Funktion ![]() gegeben ist durch die
Gamma-Funktionen:
gegeben ist durch die
Gamma-Funktionen:
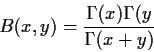 |
(3.18) |
und
![]() , und
, und
![]() ist die
Regge-Trajektorie.
ist die
Regge-Trajektorie.
Diese Amplitude hat Pole wenn die Trajektorien ganzzahlige Werte annehmen und auch das richtige asymptotische Verhalten, wie man nach der Stirling-Formel ausrechnen kann.