| (2.1) |
2.4 Erfolge und Misserfolge der Quantenfeldtheorie
Der Wechselwirkungsterm eines Nukleons mit einem pi-Meson ist:
| (2.1) |
2.7 Immer mehr neue Teilchen
In Abb. 2.12 ist auf der ![]() -Achse die ,,invariante Masse''
-Achse die ,,invariante Masse''
![]() der beiden erzeugten
der beiden erzeugten ![]() -Mesonen aufgetragen.
-Mesonen aufgetragen.
| (2.3) |
2.8 Die Überraschungen der schwachen Wechselwirkung
2.8.1 Einschub: Rechts- und Linkshändige Teilchen
Der Zusammenhang zwischen Weyl- und
Dirac-Spinoren ist gegeben durch die ![]() -Matrix (2.2):
-Matrix (2.2):
| (2.4) |
2.8.2 Zurück zur schwachen Wechselwirkung
An der schwachen Wechselwirkung nehmen nur die
linkshändigen Teilchen teil, also
![]() . Konkret heisst dies für
den Wechselwirkungsterm beim mü-Zerfall
. Konkret heisst dies für
den Wechselwirkungsterm beim mü-Zerfall
![]() :
:
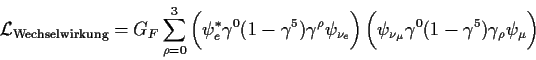 |
(2.5) |
Der Ausdruck
![]() ist ein ,, geladener schwacher
ist ein ,, geladener schwacher ![]() Strom''.
Strom''.
Geladen, weil er die Ladung ändert (vom Neutrino zum Elektron), schwach weil
er in der schwachen Wechselwirkung auftritt und ![]() weil sich der Teil
weil sich der Teil
![]() wie ein normaler Vektor und der Teil
wie ein normaler Vektor und der Teil
![]() wie ein axialer Vektor verhält.
wie ein axialer Vektor verhält.
2.8.2 Zurück zur schwachen Wechselwirkung
Bei ![]() -Verletzung setzen wir an:
-Verletzung setzen wir an:
| (2.6) |
wobei
![]() ein Mass für die
ein Mass für die ![]() -Verletzung ist. Der experimentelle
Wert dafür ist sehr klein, etwa 0.001.
-Verletzung ist. Der experimentelle
Wert dafür ist sehr klein, etwa 0.001. ![]() ist also nur sehr schwach
verletzt.
ist also nur sehr schwach
verletzt.