Drei und mehr Probleme - Eine Lösung
Schwimmende zweidimensionale Körper im Gleichgewicht,
das Radspurproblem und
Elektronen in einem parabolischen Magnetfeld
English
Franz Wegner
Institut für Theoretische Physik
Ruprecht-Karls-Universität Heidelberg
Dieser Beitrag hat einen zweifachen Zweck:
Nachdem die drei Probleme der
Arbeit
physics/0701241 (wo auch Zitate angegeben sind) erklärt sind, wird
(i) die Lösung beschrieben, wobei fast keine
Mathematik verwendet wird, und
(ii) es werden Animationen für einige dieser Lösungen
gezeigt.
Einige mathematische Formeln und Ergänzungen findet man in diesem
ps-file bzw. pdf-file.
Wir zeigen jedoch in kurzer Form, dass es mehr Probleme mit diese Lösungen
gibt, bevor wir durch das zuvor angegebene Programm gehen.
Die weiteren Fragestellungen
G. Bor, M. Levi, R. Perline, und S. Tabachnikov berichten in ihrer Arbeit
"The track geometry and integrable curve evolution"
arXiv: 1705.06314
(2017), dass die
Kurven, die die drei Probleme lösen, auch Lösung mehrerer anderer
Probleme sind.
Der lineare Grenzfall, den wir unten beschreiben, gibt die Form der Elastica wieder.
Darunter versteht man die Form eines elastischen gebogenen Drahtes.
Diese wurde von Jakob (James) Bernoulli 1691-1695 berechnet, der annahm, dass die Krümmung des Drahtes proportional zum Drehmoment ist.
1772 schlug Daniel Bernoulli (Neffe von Jakob) in einem Brief an
Leonhard Euler diesem vor, dass die potentielle Energie eines gebogenen Drahtes
proportional dem Quadrat der Krümmung integriert über die Bogenlänge des Drahtes sei.
Euler, Meister in Variations-Techniken, führte eine sehr gründliche
Berechnung der Elastica 1774 durch. Beide Ansätze sind äquivalent.
Es gibt noch weitere Probleme im Zusammenhang mit den Elastica.
Ein sehr guter Überblick findet sich in der Doktorarbeit von Raph Levien The elastica: A mathematical history.
Die geschlossenen Kurven, die wir ausführlich betrachten, haben die
Formen von eingedellten Ringen. Sie stellen Elastica unter homogenem Druck von außen dar. Lé;vy 1884, Halphen 1884-1888, und Greenhill 1892-1899
haben sie ausführlich untersucht.
Ein Überblick über diese Probleme und Lösungen findet sich
in meiner Arbeit "From Elastica to floating bodies of equilibrium"
arXiv: 1909.12596.
Den historischen Überblick dieser Arbeit mit der Angabe der verschiedenen
Probleme füge ich unter dem Titel "Von den Elastica zu den schwimmenden
Körpern im Gleichgewicht" in
deutscher Übersetzung bei.
Die drei Probleme
Schwimmende zweidimensionale Körper im Gleichgewicht
Von 1935 bis 1941 sammelten Mathematiker an der Universität in Lviv (Ukraine,
damals Lwów Polen, früher Lemberg in Österreich-Ungarn), darunter Stefan
Banach und Mark Kac, mathematische Probleme in einem Buch, das als
Schottisches Buch bekannt wurde, da sie sich oft im Schottischen Cafe
trafen. Stanislaw Ulam stellte das Problem 19 dieses Buchs: "Ist eine Kugel der
einzige Festkörper konstanter Dichte, der im Wasser in jeder Orientierung
schwimmen kann?" Das entsprechende zweidimensionale Problem, das wir hier
betrachten, lautet: Gibt es lange gerade zylindrische Körper von
nicht kreisförmigem Querschnitt, die in jeder Orientierung schwimmen
können, ohne zu rotieren? 1938 gab Herman Auerbach eine große Klasse von
Lösungen für einen Körper an, dessen Dichte die Hälfte der des Wassers
ist. Hier betrachten wir in erster Linie den Fall, in dem sich diese relative
Dichte von 1/2 unterscheidet. Am Ende gebe ich einige Beispiele für diese
Dichte.
Unter einem geraden Zylinder verstehen wir einen Körper, der von zwei
parallelen, ebenen Flächen (Grund- und Deckfläche) und einer Mantel- bzw.
Zylinderfläche, die von parallelen Geraden gebildet wird, begrenzt ist, wobei
diese Geraden senkrecht auf Grund- und Deckfläche stehen.
Das Fahrradspurproblem
Dieses Problem geht zurück auf die Geschichte "Das Abenteuer der
Internatsschule" (The Priory School) von Arthur Conan Doyle, in der Sherlock
Holmes und Dr. Watson beim Anblick der zwei Radspuren eines Fahrrads
diskutieren, in welche Richtung das Rad fuhr. Das Problem ist: Gibt es außer Kreisen und Geraden Radspuren, denen man nicht entnehmen
kann, in welche Richtung der Radler fuhr?
Zur Lösung macht man eine vereinfachende Annahme (Physiker modellieren oft
Systeme mittels Vereinfachungen): Es wird angenommen, dass die Lenksäule
senkrecht auf der Ebene steht, auf der sich das Rad bewegt.
Elektronen in einem parabolischen Magnetfeld
Ein Elektron bewegt sich in einer Ebene in einem Magnetfeld, das
senkrecht zur Ebene steht und das parabolisch ist; das heißt die Feldstärke ist
eine Konstante plus eine andere Konstante mal dem Quadrat der Entfernung vom
Ursprung. Auf
welcher Bahn bewegt sich das Elektron? Da das Elektron nur der Lorentz-Kraft
unterworfen ist, die senkrecht auf seiner Geschwindigkeit steht, ist der Betrag
seiner Geschwindigkeit konstant, aber seine Richtung ändert sich. Die Krümmung
der Bahnkurve ist proportional zur magnetischen Feldstärke.
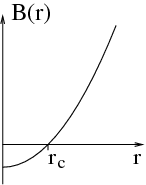 Die magnetische Feldstärke ändert ihr Vorzeichen bei rc.
Überschreitet das Elektron diese Entfernung vom Ursprung, so ändert sich dort
die Richtung der Bahnkrümmung.
Die magnetische Feldstärke ändert ihr Vorzeichen bei rc.
Überschreitet das Elektron diese Entfernung vom Ursprung, so ändert sich dort
die Richtung der Bahnkrümmung.
Die Lösung
Diese drei Probleme haben eine gemeinsame Lösung. Ich gebe hier nicht die
mathematischen Details an. Der interessierte Leser findet sie in der Arbeit
physics/0701241 (englisch). Zur Lösung benötigt man doppelt-periodische
Funktionen und
verwandte Weierstrass-Funktionen. In speziellen Fällen, die ich unten angeben
werde, kann das Ergebnis durch trigonometrische and Exponential-Funktionen
dargestellt werden. Ich werde hier jedoch hier einige Eigenschaften der
Lösungen angeben und bewegte Figuren zeigen.
Schwimmende zweidimensionale Körper im Gleichgewicht
Offensichtlich muss die Querschnittsfläche unterhalb der Wasserlinie für alle
Orientierungen des Zylinders die gleiche sein. Sie ist gegeben durch die totale
Querschnittsfläche multipliziert mit der Dichte des Körpers dividiert durch die
Dichte des Wassers (Archimedisches Prinzip).
Eine Diskussion der hydrostatischen Eigenschaften zeigt, dass die Länge der
Wasserlinie (die Linie, die den Teil des Querschnitts unter Wasser von dem
oberhalb des Wassers trennt), die ich mit 2l bezeichne, konstant ist.
Darüber hinaus ist die Länge des Umfangs des Querschnitts unter Wasser
konstant. In den Animationen wird die Begrenzung des Querschnitts in schwarz
gezeigt.
Anstatt den Körper zu rotieren, werde ich ihn festhalten und annehmen, dass die
Richtung der Gravitation rotiert. Dann werden die verschiedenen Wasserlinien in
grün und blaugrün gezeigt. Die rote Einhüllende der Wasserlinien berührt diese
Linien in der Mitte. Der Teil innerhalb der Einhüllenden ist immer oberhalb
oder unterhalb des Wassers (vorausgesetzt innerhalb und außerhalb ist wohl
definiert, was nicht der Fall ist, wenn die Dichte des Körpers die Hälfte der
Wasserdichte ist).
Das Fahrradspurproblem
Mit der oben angegebenen Vereinfachung ist der Abstand zwischen den Punkten, an
denen Vorder- und Hinterrad den Boden berühren, konstant. Wir bezeichnen ihn
mit l. Dann ergeben die Endpunkte der Tangenten
der Länge l an die Spur des Hinterrades in Richtung der Bewegung des
Rades die Spur des Vorderrades. Falls diese Tangenten in beiden Richtungen an
der Spur des Vorderrades enden, ist offen, in welche Richtung das Rad
fuhr. Daher haben wir es nun mit dem gleichen Problem wie beim schwimmenden
Körper zu tun.
Jetzt sind die schwarzen Linien die Spuren des Vorderrades, die roten Linien die
Spuren des Hinterrades, und die sich verschiebenden grünen und blaugrünen Linien
geben die Lage der Fahrräder zu verschiedenen Zeiten an.
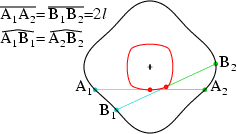
Eigenschaft der konstanten Sehnenlänge
Wir suchen und finden daher Kurven, die die folgende Eigenschaft der konstanten
Sehnenlänge haben: Ausgehend von zwei geeigneten Punkten A1 und
A2 auf der Kurve bewegen wir uns eine beliebige, aber gleiche
Bogenlänge auf den Kurven zu den Punkten B1 und B2. Dann
muss die Sehnenlänge die gleiche sein, A1A2 =
B1B2 = 2l.
Zur Lösung
Ursprünglich betrachtete ich das Problem der schwimmenden Körper. Ich begann mit
dem Kreis, einer offensichtlichen Lösung. Dann verbog ich ihn leicht, indem ich
dem Abstand vom Ursprung erlaubte, zu oszillieren, so dass bei einem Umlauf der
Radius n mal
etwas größer, n mal etwas kleiner als der mittlere Radius war. Dies ergibt
Lösungen für n-2 verschiedene Dichten. Dann entwickelte ich das Ergebnis nach
Potenzen der Verbiegung (Taylor-Entwicklung) und ich stellte fest, soweit ich
die Entwicklung durchführen konnte, dass diese Entwicklung für alle n-2
verschiedenen Dichten übereinstimmte. Diese Entwicklung erforderte umfangreiche
analytische Rechnungen. Es war daher nützlich ein Computeralgebra-System
(Maple) zu verwenden. Die Annahme, dass diese Unabhängigkeit auch in höheren
Ordnungen gilt, gab mir einen Hinweis darauf, wie man eine
Differentialgleichung für die Begrenzungslinie herleiten kann.
Elektronen in einem parabolischen Magnetfeld
Integriert man diese Differentialgleichung einmal, so findet man, dass die
Krümmung der Begrenzungskurve quadratisch vom Radius abhängt. Dies wurde mir
allerdings erst klar, nachdem ich die Bahnen von Elektronen sah, die sich in
einem linear anwachsenden Magnetfeld bewegen, das senkrecht zur Ebene steht.
Diese waren von Evers, Mirlin, Polyakov und Wölfle berechnet worden, und
sahen den Kurven, die ich im entsprechenden linearen Grenzfall berechnet hatte,
sehr ähnlich.
Verschiedene Bedingungen
Die Kurven, die ich im folgenden zeigen werde, sind Lösungen einer
Differentialgleichung, die mehrere Konstanten enthält, die so gewählt werden
können, dass bestimmte Bedingungen für die Kurve erfüllt sind. Im Falle des
sich bewegenden Elektrons gibt es keine Einschränkungen.
Im Falle der Radspuren wird man im allgemeinen davon ausgehen, dass sie/er in
einer Richtung fährt; insbesondere sollte das für die Bewegung des Hinterrads
zutreffen. Falls sie/er sehr artistisch ist und das Rad es erlaubt, dann gibt
es auch Fälle, in denen sie/er sich vor und zurück bewegt. Für einige Lösungen
ist es sogar notwendig, dass man die Lenkstange um mehr als 180 Grad drehen
kann. Trotzdem kann es sein, dass Teile der Kurve ohne Probleme durchradelt
werden können. Schließlich fahren Radler nicht unbegrenzt.
Für die Begrenzung des schwimmenden Körpers muss man fordern, dass sie
geschlossen und der Querschnitt hinreichend konvex ist, so dass die
Wasserlinien die Begrenzung genau zweimal schneiden, und nicht öfter.
Eigenschaft der konstanten Entfernung
Die Klasse von Kurven, die hier beschrieben werden, haben eine bemerkenswerte
Eigenschaft: Man wähle willkürlich zwei Punkte A'1 und A2
auf der schwarzen Kurve. Dann gibt es einen Winkel δχ, um den diese
Kurve in die blaue Kurve zu drehen ist, wobei A'1 nach A1
gedreht wird. Geht man nun von A1 und A2 auf den
jeweiligen Kurven beliebige, aber gleiche Bogenlängen entlang, so ist der
Abstand zwischen den neuen Punkten B1 und B2 der gleiche,
A1A2 = B1B2 = 2l.
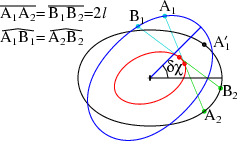
Ich nenne dies die Eigenschaft der konstanten Entfernung.
Falls A1 und A2 übereinstimmen, dann ist der Winkel
δχ=0.
Er wächst mit dem Abstand der Punkte A'1 und A2 auf
der Kurve an. Jedes mal, wenn dieser Winkel δχ die beiden Kurven zur
Deckung bringt, fallen die schwarze und die blaue Kurve
zusammen und man erhält eine Lösung für die Sehnen konstanter Länge.
In dem Beispiel mit verschiedenen Drehwinkeln
δχ ist das bei δχ=900 der Fall.
Diese Eigenschaft machte es möglich, eine Differentialgleichung für die Kurven
zu erhalten, indem das Problem für einen sehr kleinen Winkel δχ
betrachtet wurde.
(Eine Animation für zwei Drehwinkel wird hier unten
gezeigt).
Zweige und Grenzfälle
Je nach Wert der Konstanten in der Differentialgleichung erhält man einen
Kurvenzweig oder zwei. Dies sollte nicht zu überraschend sein, da man für
Kegelschnitte etwas entsprechendes hat. Dort kann man Ellipsen (ein Zweig) oder
Hyperbeln (zwei Zweige) als Lösungen haben. Man bemerkt außerdem, dass es für
Kegelschnitte gewisse Grenzfälle gibt. Ein solcher Grenzfall ist die Parabel (an
der Grenze zwischen Ellipse und Hyperbel), ein anderer Grenzfall ergibt zwei
Geraden (bei einem Schnitt durch die Spitze des Kegels).
Ähnlich gibt es hier zwei Grenzfälle: In einem ist der Kreis Lösung oder die
Kurve nähert sich ihm asymptotisch; der andere ist der lineare Grenzfall, bei
dem sich die Kurven periodisch in gerader Richtung wiederholen.
Die Form eines Kegelschnitts kann durch eine Zahl beschrieben werden, die
kontinuierlich variiert werden kann. Für Ellipsen kann das das Verhältnis
zwischen den beiden Hauptachsen sein. (Allgemein verwendet man zur
Charakterisierung der Form der Kegelschnitte die numerische
Exzentrizität). Die Form unserer Kurven ist durch zwei
Zahlen festgelegt, die kontinuierlich variiert werden können.
Die meisten Kurven wiederholen sich nach Rotation um einen bestimmten Winkel
ψr. Daher kann eine dieser Zahlen dieser Winkel sein. Hier werde
ich meist Figuren zeigen, die geschlossen sind. Dies ist der Fall, falls
ψr=3600×m/n mit ganzen (teilerfremden) m und n.
Daher wiederholen sich die Kurven nach m-fachen Umlauf um den Ursprung. Während
dieser m Umläufe erreicht die Kurve n mal ihre größte und n mal ihre geringste
Entfernung vom Zentrum der Kurve.
Für das Problem des schwimmenden Körpers benötigt man m=1.
Eine andere Größe, die variiert werden kann, ist das Verhältnis des größten und
kleinsten Abstands vom Ursprung, den ich als (1+ε)/(1-ε)
einführe.
Dreidimensionale Körper
Das ursprüngliche Problem lautete "Ist eine Kugel der einzige Festkörper
konstanter Dichte, der im Wasser in jeder Orientierung schwimmen kann?" Hierzu
gibt es den Beweis von Schneider und von Falconer, dass ein sternförmiger
zentralsymmetrischer Körper, der in allen Orientierungen bei Dichte 1/2
schwimmen kann, eine Kugel sein muss. Sternförmig heißt ein
Körper, wenn es einen Punkt A gibt, sodass für jeden Punkt P im
Körper die gerade Verbindungslinie AP vollständig im Inneren des
Körpers verläuft. Bisher habe ich zwei Untersuchungen zum Problem der
dreidimensionalen Körper durchgeführt. In beiden Fällen
betrachte ich kleine Deformationen um die Kugel:
In arxiv: 0803.1043 mit
dem Titel "Floating Bodies of Equilibrium in Three Dimensions. The central
symmetric case" werden die Bedingungen für Körper mit
Zentralsymmetrie und relativer Dichte verschieden von 1/2 untersucht. Es wird
aber auch an einem Beispiel gezeigt, dass es zentralsymmetrische Lösungen
zu dieser Dichte gibt, wenn man die Bedingung der Sternform fallen
lässt.
In arxiv: 0902.3538
mit dem Titel "Floating Bodies of Equilibrium at Density 1/2 in Arbitrary
Dimensions" wird gezeigt, dass es auch in Dimension drei (und höher) eine
große Mannigfaltigkeit von Lösungen zur Dichte 1/2 gibt. Zu jeder
gegebenen Einhüllenden der Wasserflächen, die nur die Eigenschaft
haben muss, dass es genau eine Tangentialebene an die Einhüllende parallel
zu jeder Ebene gibt, gibt es Lösungen.
Gegenwärtig führe ich Untersuchungen zu nicht zentralsymmetrischen
Körpern mit Dichte verschieden von 1/2 durch.
Die Animationen
Wie in den obigen Figuren werden der Rand des schwimmenden Körpers, die Spur des
Vorderrades und die Bahn der Ladung in schwarz und manchmal in blau
dargestellt. Die Wasserlinie des schwimmenden Körpers wird halb in grün, halb
in blaugrün dargestellt. Diese beiden Linien geben auch die Lage der beiden
Fahrräder in grün und blaugrün wieder. Die grünen und blaugrünen Endpunkte
bewegen sich
auf der schwarzen (blauen) Kurve und geben die Lage der Vorderräder der beiden
Fahrräder an. Der Mitte (roter Punkt) der Linie generiert die rote
Einhüllende. Sie ist die Spur des Hinterrades. Die grünen und blaugrünen
Endpunkte
bewegen sich in jedem Schritt um die gleiche Bogenlänge auf der schwarzen
(blauen) Kurve. Die Länge l der grünen und blaugrünen Linien sind
konstant.
Beispiele für schwimmende Körper
Hier werden einige Lösungen für
schwimmende Körper für n=4, 5, und 6 gezeigt.
Man beachte, dass im allgemeinen ein gegebener Querschnitt Lösung für mehrere
Dichten ist.
Natürlich sind dies auch Lösungen für das Fahrradspurproblem.
Man vergleiche dies mit den
Beispielen von David L. Finn.
Variation des Verhältnisses der extremen Radien
Damit die Querschnitte der schwimmenden Körper hinreichend konvex sind, muss
ε hinreichend klein sein. Dies gilt auch für das Fahrradspurproblem, da
sonst die/der Radler(in) gezwungen ist mit dem Hinterrad vor und zurück zu
fahren. In den Figuren für die schwimmenden Körper war ε=0.1 für
n=4 und n=5, ε=0.05 für n=6.
Hier zeigen wir Figuren für größere Werte von ε für
n=5.
Falls ε=1 ist, geht die Kurve durch den Ursprung. Für größere Werte von
ε führt sie auf der anderen Seite am Ursprung vorbei und das Verhältnis
aus größtem und kleinstem Abstand ist (1+ε)/(ε-1).
Eigenschaft des konstanten Abstands
Die Eigenschaft des konstanten Abstands, die oben erwähnt
wurde, wird in zwei Beispielen für m/n=1/2
gezeigt.
Es sei noch bemerkt, dass man keine Sehne konstanter Länge erhält, wenn n-m=1
ist, was also hier der Fall ist. Doch bleibt die Eigenschaft des konstanten
Abstands.
m≠1 und die Acht
m muss nicht gleich 1 sein. Die erste Figur in m≠1,
die Acht
zeigt ein Beispiel für m/n=2/5 mit Sehne konstanter Länge.
Die anderen zwei Figuren zeigen Paare von Achten, die man für m=0
erhält, die durch Linien konstanter Länge verbunden sind.
Für diese Achten hat man m/n=0/1. Daher gibt es auch für diese keine Sehnen
konstanter Länge.
Aus Gründen, die ich hier nicht erkläre, kann man auch negative m verwenden.
Ein Beispiel für m/n=-1/7 mit drei verschiedenen
Sehnenlängen wird gezeigt.
Beispiel mit zwei Zweigen
Wie vorher erwähnt, können zu den Kurven zwei Zweige gehören. Dann besteht nicht
nur innerhalb der einzelnen Zweige die Eigenschaft des konstanten Abstands,
sondern auch zwischen den beiden Zweigen. Dies wir für
m/n=1/3, ε=3.0 gezeigt.
Der ausgeartete Fall mit Kreisen
Auf den folgenden fünf Seiten werden Kurven gezeigt, die dadurch erzeugt werden
können, dass man das blaugrüne Ende einer Strecke entlang des magentaroten
Kreises so bewegt, dass die rote Mitte der Strecke sich in Richtung der
Strecke bewegt, als ob die Strecke in der Mitte von einem Rad unterstützt ist,
das in Richtung der Linie angebracht ist. Das andere grüne Ende der Linie
beschreibt die gesuchte Kurve.
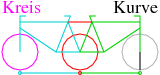
Hier nützen wir aus, dass der Kreis eine der
beiden Kurven ist, bzw. sich die Kurve asymptotisch annähert. Daher besteht
hier die Eigenschaft des konstanten Abstandes zwischen Kreis und nicht
trivialer Kurve.
Diese Lösungen können durch Exponential- und
trigonometrische Funktionen (siehe Abschnitt 8 der Arbeit) dargestellt werden,
während sonst doppel-periodische Funktionen benötigt werden.
Auf den folgenden drei Webseiten zeigt die erste Figur diese Konstruktion, die
zweite die Bewegung der Sehne. Dies sind keine Lösungen für den schwimmenden
Körper, aber Teile der schwarzen und roten Kurven, die den Schleifen entkommen,
sind Lösungen für die Fahrradspuren.
ε ist das Verhältnis der Länge der Linie zum Radius des magentaroten
Kreises für die jeweils erste Figur. Falls ε größer als zwei ist, dann
ist die
erzeugte schwarze Kurve periodisch. Drei εs wurden ausgewählt, um
geschlossene Kurven zu erzeugen:
m/n=1/3, ε=5/2=2.5
m/n=-1/3, ε=sqrt(49/10)=2.213594
m/n=-2/1, ε=sqrt(64/15)=2.065591
Falls ε kleiner als zwei ist, erhält man eine Kurve außerhalb und eine
innerhalb des Kreises.
In diesem Fall nähert sich die Kurve asymptotisch an den Kreis. Wir zeigen die
Kurven für ε=1.6.
Im Grenzfall ε=2 erhält man eine Kurve, die
sich asymptotisch an den Kreis annähert.
Der lineare Grenzfall
Man kann die extremen Abstände vom Ursprung nach unendlich gehen lassen, aber
deren Differenzen endlich lassen. Dann erhält man den linearen Grenzfall.
Auch hier gibt es mehrere Möglichkeiten. Man kann einen Kurvenzweig erhalten.
So lange die Kurven so lang gezogen sind wie im Beispiel, handelt es sich um
gute Lösungen für das Radspurproblem.
Im Grenzfall extremer Streckung
gibt es keine Lösung für eine Sehne konstanter Länge. Es gibt jedoch Linien
konstanter Länge für zwei Kurven, die gegeneinander verschoben sind oder
einander gegenüber liegen.
Die Kurve entsteht auch, indem man das blaugrüne Ende der Strecke an der
magentaroten
Geraden entlang laufen lässt, sie so bewegt, dass die Mitte wieder parallel zur
geraden läuft. Dann durchläuft das grüne Ende die schwarze Kurve.
Im linearen Grenzfall gibt es auch den Fall zweier
Kurvenzweige.
Zwischen diesen gibt es Linien konstanten Abstands für unendlich viele
Abstände.
Derartige Kurven finden sich in einer Arbeit von
Evers, Mirlin, Polyakov, und
Wölfle (siehe Figuren 1 und 2) als Elektronenbahnen in einem
magnetischen Feld senkrecht zur Ebene, das linear in einer Richtung der Ebene
anwächst.
Die Karusselle von Oliveros, Montejano and Bracho
Oliveros, Montejano und Bracho führen fünf dynamische gleichseitige (aber nicht
gleichwinklige) Fünfecke ein, deren Ecken auf einer oder fünf gleichen Kurven
laufen, wobei die Seiten des Fünfecks Sehnen oder Strecken konstanter Länge
bilden. (Sie bezeichnen diese Anordnung als Karussell).
In Karusselle I laufen die Ecken der
Fünfecke auf fünf Achten und entlang geschlossener Kurven mit m/n=1/7 and
1/12. Die Fläche der Fünfecke bleibt konstant.
In Karusselle II sind fünf Kopien
einer Kurve mit ε=1 zu sehen, die gegeneinander mit zwei verschiedenen
Winkel verdreht sind und die Ecken der Fünfecke tragen. Zusätzlich ist ein Satz
von fünf Kurven des linearen Grenzfalls zu sehen, auf denen das Fünfeck entlang
krault.
Falls sich das Fünfeck überschneidet, ist die Differenz der beiden Flächen
konstant.
Lösungen zur Dichte 1/2
Auerbach hat 1938 die allgemeine Lösung zur Dichte 1/2 angegeben.
Hierzu ist eine Einhüllende mit der Eigenschaft zu wählen, dass sie
nur eine Tangente für jede Richtung hat und nachdem die Richtung der
Tangente um 1800 gedreht ist, sich wieder schließt. Eine
solche Einhüllende hat in der Regel eine ungerade Anzahl von Spitzen.
Sie kann zum Beispiel aus Kreisbogen bestehen.
Diese Einhüllenden können auch zu
Polygonen entarten. Eines mit fünf Spitzen ist
ein Pentagramm.
Die Begrenzungen müssen keine Ecken haben. Eines der
Beispiele von Auerbach hat Herzform. Das andere hat
keine Ecken. Die Beispiele bestehen aus zwei oder drei geraden Linien und
ebensoviel gegenüberliegenden gekrümmten Linien. Diese sind
Stücke aus den
Linien, die wir oben als Grenzfall extremer Streckung hatten.
Hier sind weitere Beispiele ohne Ecken.
Im allgemeinen sind die Lösungen für die Dichte 1/2 keine
Lösungen mehr für die Bahnen von Elektronen in einem parabolischen
Magnetfeld. Sie sind immer noch Lösungen für das Fahrradspurproblem,
wenn der Radler artistisch genug ist, mit seinem Fahrrad vorwärts und
rückwärts zu fahren.
Zurück zum Anfang
 Die magnetische Feldstärke ändert ihr Vorzeichen bei rc.
Überschreitet das Elektron diese Entfernung vom Ursprung, so ändert sich dort
die Richtung der Bahnkrümmung.
Die magnetische Feldstärke ändert ihr Vorzeichen bei rc.
Überschreitet das Elektron diese Entfernung vom Ursprung, so ändert sich dort
die Richtung der Bahnkrümmung.


