Gravitational Lensing
Light Deflection
The General Theory of Relativity explains gravity in terms of assemblies of mass and energy curving space-time. This implies that masses deflect light in a way similar to a convex lens: they curve light rays towards themselves (right-hand image).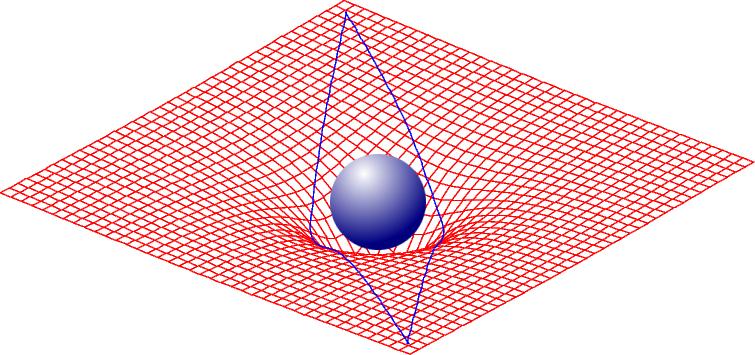
The deflection of light rays from their otherwise straight paths can
give rise to multiple images because light rays can now pass masses
in multiple ways. In addition, the deflection is differential,
i.e. light bundles can be deformed and focused as they pass
masses. Magnification, de-magnification and distortion of the
observable images are among the possible consequences.
Stars
This so-called gravitational lensing effect can be observed with objects on all mass scales. Stars can produce multiple images whose angular separations are of order micro-arc seconds. Such image splittings are unobservable, but the magnification is which accompanies them. In that way, objects can be discovered which are of stellar mass but shine only weakly or not at all. For instance, this so-called microlensing effect was employed for demonstrating that there are dark, compact objects surrounding our Milky Way galaxy.Galaxies
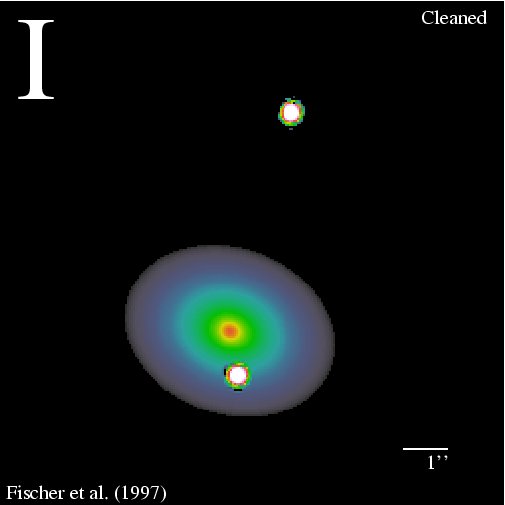Galaxies can produce multiple images with angular separations on the
order of arc seconds. The very first gravitational lens to be detected
in 1979 is an example: the quasar QSO 0957+561 (right-hand image) is
split by a galaxy into two images separated by 6 arc
seconds. Meanwhile, dozens of such multiply-imaged quasars have become
known. In some of them, quadruple images occur in complicated
configurations (image below). These images can be used for exactly
measuring the masses and mass distributions of galaxies.
The ways which light has to travel from the source typically differ in
length for the individual images of a multiply-imaged quasar. If the
source is variable, as many quasars are, the variations occur at
different times in the different images. If a model can be constructed
for the mass distribution in the gravitational lens, the Hubble
constant can be computed from the difference in light-travel
time. This can be used for calibrating cosmological distances.
Galaxy Clusters
Even galaxy clusters can act as
gravitational lenses. They contain some 100 up to of order 1000
galaxies, but consist mainly of dark matter. Some galaxy clusters can
produce highly distorted multiple images of distant galaxies which
then appear as arc-like features (arcs; the right-hand image
shows the galaxy cluster MS 2137). This effect allows the mass
distribution of the galaxy clusters to be probed, but also the
cosmological model to be tested. In addition, occasionally the
properties of very distant sources can only be measured because of the
magnification by galaxy clusters.
Veritable maps of the dark-matter distribution in galaxy clusters can
be constructed from the weaker distortion of very many galaxies in
their background. This enables mass determinations, but also analyses
of the structure of galaxy clusters.
The Universe as a Lens
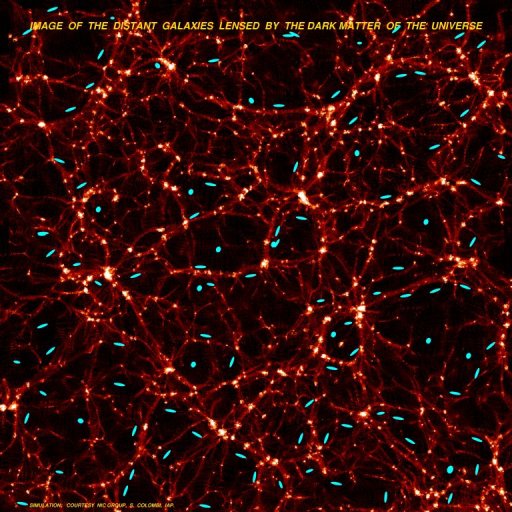The entire Universe is traversed by a filamentary network of cosmic
structures which reach lengths of some 10 million light years. Galaxy
clusters are located at the intersections of the filaments. Those
largest cosmic structures also exert a weak gravitational lensing
effect on the light of very distant sources (the left-hand image shows
an exaggerated simulation). Only in the past few years has it become
possible to measure this lensing effect; in part due to magnification,
but largely due to distortion effects. This so-called cosmic shear
allows the distribution and amount of the dark matter in the Universe
to be determined and the geometry of the Universe to be constrained.
Many more applications of the gravitational lensing effect have
meanwhile been developed. As it is solely determined by the mass
distribution of cosmic objects and neither depends on the type of
matter nor on its physical state, it has developed into one of the
most versatile tools in extragalactic astronomy and cosmology.
Verantwortlich: Matthias Bartelmann